Эпициклоидальное зацепление: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Die Seite wurde neu angelegt: {{Редактирование}} '''Эпициклоидальное зацепление''' {{другие языки|[[|de]]|[[|en]]|[[|nl]]}} [[Bild:Zykloide_Epizykl... |
WWWIG (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Редактирование}} | {{Редактирование}} | ||
'''Эпициклоидальное зацепление''' | '''Эпициклоидальное зацепление''' | ||
{{другие языки|[[de]]|[[en]]|[[nl]]}} | <!--{{другие языки|[[de]]|[[en]]|[[nl]]}}--> | ||
[[Bild:Zykloide_Epizykloide-Gypozykloide-Evolvente.jpg|thumb|A - эпициклоида; B - гипоциклоида; C - эвольвента]] | [[Bild:Zykloide_Epizykloide-Gypozykloide-Evolvente.jpg|thumb|A - эпициклоида; B - гипоциклоида; C - эвольвента]] | ||
Эпициклоида образуется качением без скольжения производящей окружности R по основной (делительной) окружности Q, когда центр производящей окружности О расположен вне основной окружности (рис. A). При качении точка А, находящаяся на производящей окружности, при совмещении точки А2 с точкой А х опишет дугу эпициклоиды ОхА. | Эпициклоида образуется качением без скольжения производящей окружности R по основной (делительной) окружности Q, когда центр производящей окружности О расположен вне основной окружности (рис. A). При качении точка А, находящаяся на производящей окружности, при совмещении точки А2 с точкой А х опишет дугу эпициклоиды ОхА. | ||
[[Bild:Epizikloide.jpg|thumb|эпициклоида]] | |||
{{Информационный блок переводов |Titel=|TNR=| | {{Информационный блок переводов |Titel=|TNR=| | ||
Англ1=|Англ2=| | Англ1=|Англ2=| | ||
Aktuelle Version vom 29. Juli 2011, 06:56 Uhr
Эпициклоидальное зацепление
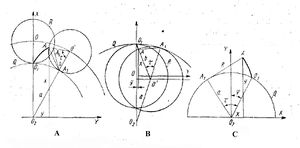
Эпициклоида образуется качением без скольжения производящей окружности R по основной (делительной) окружности Q, когда центр производящей окружности О расположен вне основной окружности (рис. A). При качении точка А, находящаяся на производящей окружности, при совмещении точки А2 с точкой А х опишет дугу эпициклоиды ОхА.

| |||||||||||||||||||||||||||
